Add picture to stat section
Showing
- 07-basic_statistics.qmd 8 additions, 4 deletions07-basic_statistics.qmd
- img/Stat_Confounders.jpg 0 additions, 0 deletionsimg/Stat_Confounders.jpg
- img/Stat_order_effects.png 0 additions, 0 deletionsimg/Stat_order_effects.png
- public/07-basic_statistics.html 19 additions, 9 deletionspublic/07-basic_statistics.html
- public/07-basic_statistics_files/figure-html/LocalMoransI_plt-1.png 0 additions, 0 deletions...basic_statistics_files/figure-html/LocalMoransI_plt-1.png
- public/07-basic_statistics_files/figure-html/MoransI-1.png 0 additions, 0 deletionspublic/07-basic_statistics_files/figure-html/MoransI-1.png
- public/07-basic_statistics_files/figure-html/cases_visualization-1.png 0 additions, 0 deletions...ic_statistics_files/figure-html/cases_visualization-1.png
- public/07-basic_statistics_files/figure-html/distribution-1.png 0 additions, 0 deletions.../07-basic_statistics_files/figure-html/distribution-1.png
- public/07-basic_statistics_files/figure-html/inc_visualization-1.png 0 additions, 0 deletions...asic_statistics_files/figure-html/inc_visualization-1.png
- public/07-basic_statistics_files/figure-html/kd_test-1.png 0 additions, 0 deletionspublic/07-basic_statistics_files/figure-html/kd_test-1.png
- public/07-basic_statistics_files/figure-html/plt_clusters-1.png 0 additions, 0 deletions.../07-basic_statistics_files/figure-html/plt_clusters-1.png
- public/img/Stat_Confounders.jpg 0 additions, 0 deletionspublic/img/Stat_Confounders.jpg
- public/img/Stat_order_effects.png 0 additions, 0 deletionspublic/img/Stat_order_effects.png
- public/search.json 3 additions, 3 deletionspublic/search.json
- public/site_libs/bootstrap/bootstrap.min.css 1 addition, 1 deletionpublic/site_libs/bootstrap/bootstrap.min.css
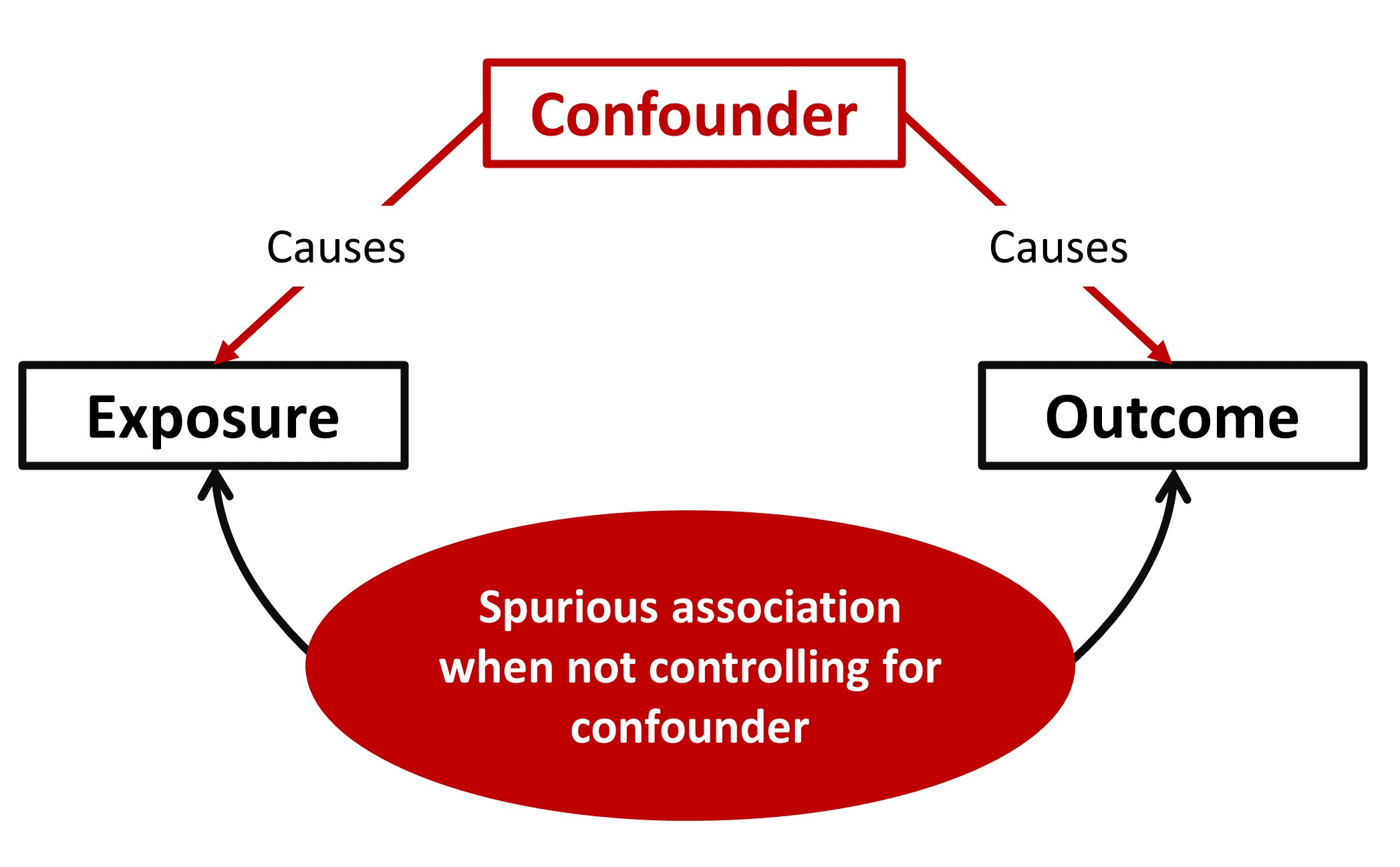
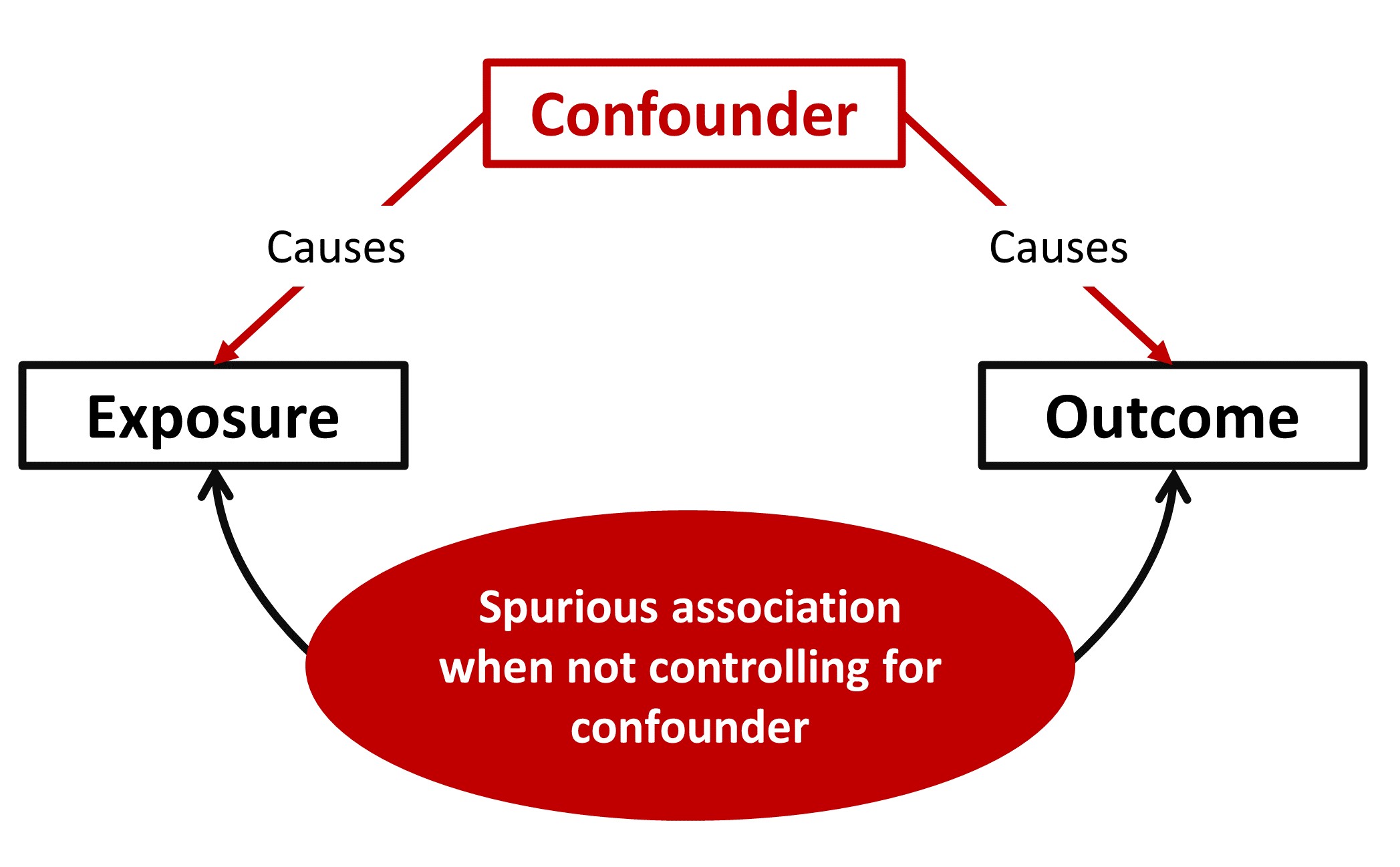
img/Stat_Confounders.jpg
0 → 100644
210 KiB
img/Stat_order_effects.png
0 → 100644
367 KiB

| W: | H:
| W: | H:



| W: | H:
| W: | H:



| W: | H:
| W: | H:



| W: | H:
| W: | H:



| W: | H:
| W: | H:



| W: | H:
| W: | H:



| W: | H:
| W: | H:


public/img/Stat_Confounders.jpg
0 → 100644
210 KiB
public/img/Stat_order_effects.png
0 → 100644
367 KiB
This diff is collapsed.
This diff is collapsed.